如何不用递归遍历二叉树

来源：

其实递归的底层实现就是栈

看完本篇大家可以使用迭代法，再重新解决如下三道leetcode上的题目：

• 144. 二叉树的前序遍历
• 94. 二叉树的中序遍历
• 145. 二叉树的后序遍历

为什么可以用迭代法（非递归的方式）来实现二叉树的前后中序遍历呢？

我们在栈与队列：匹配问题都是栈的强项中提到了，「递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中」 ，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

此时大家应该知道我们用栈也可以是实现二叉树的前后中序遍历了。

前序遍历（迭代法）

我们先看一下前序遍历。

前序遍历是中左右，每次先处理的是中间节点，那么先将跟节点放入栈中，然后将右孩子加入栈，再加入左孩子。

为什么要先加入 右孩子，再加入左孩子呢？因为这样出栈的时候才是中左右的顺序。

动画如下：

不难写出如下代码:

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                      // 中
            st.pop();
            if (node != NULL) result.push_back(node->val);
            else continue;
            st.push(node->right);                           // 右
            st.push(node->left);                            // 左
        }
        return result;
    }
};

此时会发现貌似使用迭代法写出前序遍历并不难，确实不难。

「此时是不是想改一点前序遍历代码顺序就把中序遍历搞出来了？」

其实还真不行！

但接下来，「再用迭代法写中序遍历的时候，会发现套路又不一样了，目前的前序遍历的逻辑无法直接应用到中序遍历上。」

中序遍历（迭代法）

为了解释清楚，我说明一下 刚刚在迭代的过程中，其实我们有两个操作：

1. 「处理：将元素放进result数组中」
2. 「访问：遍历节点」
   分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，「因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。」

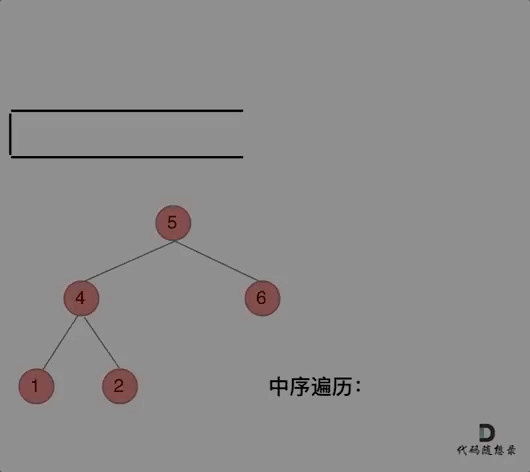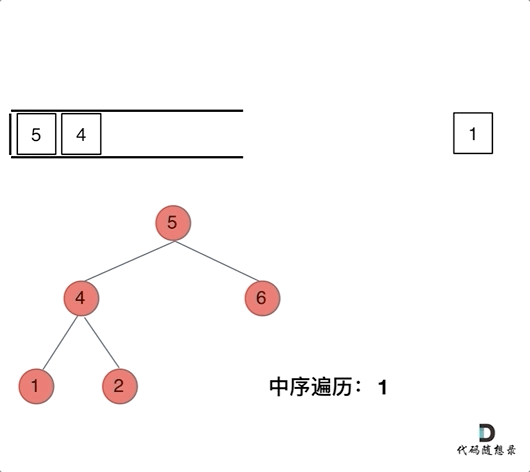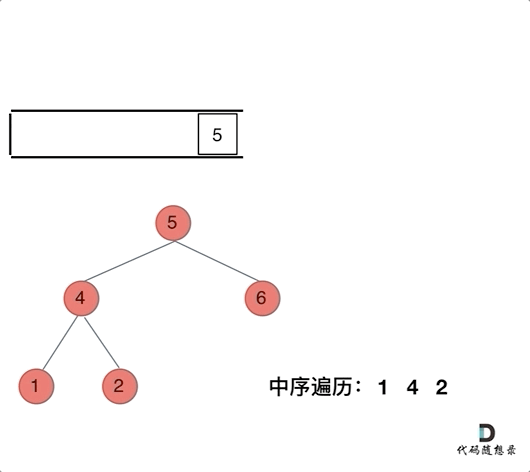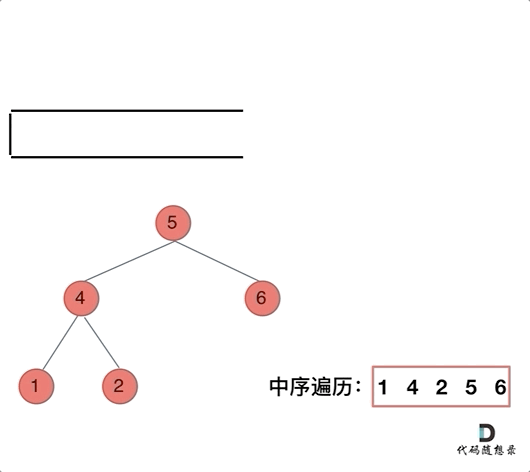
那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了**「处理顺序和访问顺序是不一致的。」**

那么**「在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。」**

动画如下：

「中序遍历，可以写出如下代码：」

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 讲访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};

后序遍历（迭代法）

再来看后序遍历，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：

「所以后序遍历只需要前序遍历的代码稍作修改就可以了，代码如下：」

class Solution {
public:

    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            if (node != NULL) result.push_back(node->val);
            else continue;
            st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序
            st.push(node->right);
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

总结

此时我们用迭代法写出了二叉树的前后中序遍历，大家可以看出前序和中序是完全两种代码风格，并不想递归写法那样代码稍做调整，就可以实现前后中序。

「这是因为前序遍历中访问节点（遍历节点）和处理节点（将元素放进result数组中）可以同步处理，但是中序就无法做到同步！」

上面这句话，可能一些同学不太理解，建议自己亲手用迭代法，先写出来前序，再试试能不能写出中序，就能理解了。